The FAIR model is a powerful tool for analyzing risk on its own but the RiskLens platform pairs it with a Monte Carlo risk simulation analysis engine that runs your data through a vast range of scenarios to produce the clearest view of the probable outcomes you face, even with limited data.
Monte Carlo may look like a black box, but in this video, RiskLens consultant David Musselwhite makes its inner workings—and its usefulness—as easy to understand as counting calories over the holiday season. (You can also read a transcript below.)
Definition: What Is Monte Carlo Risk Simulation for Cybersecurity?
The RiskLens platform's Monte Carlo risk simulation tools determine from your inputs for a given loss event scenario...
- Number of primary loss events that may occur and their costs in primary losses (such as incident response)
- Number of secondary loss events that may occur, and how much each of those will cost in secondary losses (such as legal costs)
Adding those events and their associated losses together derives an estimated amount of risk.
By evaluating this formula thousands of times using different inputs drawn from the distributions you defined in the RiskLens platform for the variables of the FAIR model, Monte Carlo simulation allows us to see the range of outcomes in dollar terms that are possible and their relative probabilities.
How Is Monte Carlo Risk Simulation Analysis Reported?
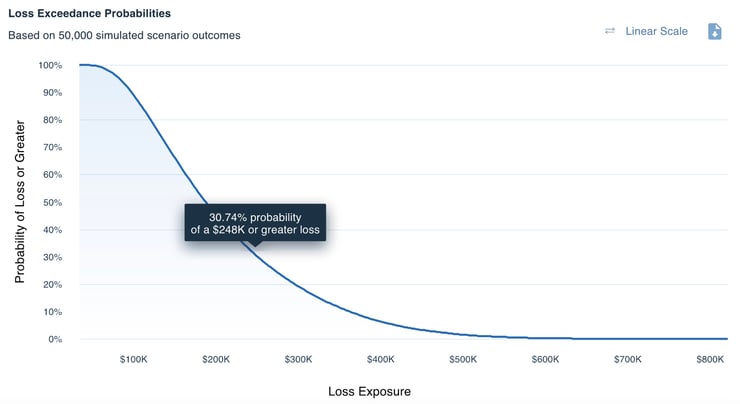
The RiskLens platform displays analysis results as annualized loss exposure (ALE) in a variety of formats including this loss exceedance curve showing in a range the probability of a particular amount of loss materializing.
Learn more:
What Does RiskLens Risk Reporting Tell Me?
Do I Have to Be a Math Nerd to Perform FAIR Analysis?
TRANSCRIPT
Monte Carlo simulation is used in many risk analysis methodologies, including FAIR. But how does it work? Many people intimidated by math and statistics get defensive and assume they won’t be able to understand Monte Carlo, but I assure you that isn’t the case.
Monte Carlo simulation is a method for performing calculations when you have uncertainty about the inputs. Since the holiday season is approaching, let’s say I want to forecast the number of calories I will consume from eating holiday cookies. If I think back to previous years, I’d say my best guesses are that I will attend 2 parties, that I’ll eat 5 cookies at each party, and that each cookie will contain 50 calories. Multiplying these together, I’d forecast that I will consume 500 calories worth of holiday cookies.
Learn FAIR quantitative risk analysis from the experts - the RiskLens Academy
But is that model really the best I can do? Don’t I have some uncertainty about each of the variables? Maybe this year I’ll get invited to more or fewer parties. Since I’ve been running more since last year and my metabolism has sped up, maybe I’ll feel less guilty and eat more cookies at each party. And with the variety of ingredients and sizes of cookies available, does it really make sense to assume they will all be 50 calories? Instead of using single numbers, or point-estimates, as we call them, I can get a more accurate idea of how many calories I might consume by estimating values for each of these variables using a range.
Let’s say I will get invited to between 1 and 4 parties, but most likely 2, and that at each party I will eat between 4 and 8 cookies, but most likely 5, and that each cookie will contain between 35 and 120 calories, but most likely 50. Now I have accounted for my uncertainty about the future by using ranges instead of point-estimates.
Instead of just performing the calculation once with my point-estimates, Monte Carlo simulation is going to perform the calculation thousands of times using values it chooses at random from the distributions I’ve defined. One run, or iteration, of the Monte Carlo might say I’ll be invited to 3 parties, eat 7 cookies at each, and that each cookie will contain 40 calories. All of these values are within the range of possibilities I’ve defined, so the result, consumption of 840 calories, is possible. In another iteration, I may only get invited to 1 party and consume 4 cookies, each of which contains 80 calories, meaning I will have consumed 320 calories.
Why would I want to say that 500 calories is my definitive forecast when I know there are a range of possibilities, including consuming 320 calories, or maybe even 840 if I really let myself go? It is far more valuable to accurately report a range of outcomes than it is to report a single precise outcome that is almost certain to be wrong.
Monte Carlo simulation works exactly the same way using FAIR and the RiskLens platform. Instead of using point estimates to say we will have 4 loss events over the next year, and each one will cost us $300,000, we define ranges for these inputs and let the Monte Carlo simulation identify tens of thousands of possible outcomes. We then put all of those outcomes on a graph so we can see where our total loss exposure is more likely to fall.
Monte Carlo simulation shouldn’t be intimidating once you understand that it is just a way to say, “I don’t know the exact value of this input, but I still want to perform calculations assuming that the value will fall between this minimum and this maximum, and that I think it is most likely to be this number.” Looking at the distribution of possible outcomes doesn’t allow you to say, “I know with precision what the answer will be,” but it does allow us to say, “I know the answer should fall within this range.” When making calculations that will inform decisions about the future, we should always value accuracy over precision.
What questions do you have about Monte Carlo simulation? What aspects of it, or the way it’s used with FAIR and the RiskLens platform, are still unclear? What value have you gotten from moving away from point estimates and toward ranges and Monte Carlo simulation? Join the conversation — leave a comment below.
Schedule a demo to see how quantitative cyber risk analysis can work for your organization