I want to address a growing concern I have with other risk quantification software solutions. My concern is rooted in the idea that we can predict future cybersecurity events with some high degree of confidence. What's interesting about that idea is nobody explicitly states they are predicting the future. If they did, cybersecurity professionals would laugh the purveyors out of the room! So, why do we as cybersecurity professionals not recognize it when it's slathered with beautiful chromatic reporting or explained away with complex mathematical formulas? What I'm talking about is the problem of precision.
What is precision?
Let's level-set on that word for a moment. Precision is all about exactness. Think of it like this: when you step on the scale in the morning you expect a precise weight reported to you. It's exact. Resolute. When we approach cybersecurity risk in this manner, we make a terrifying mistake: we assume, like your body weight, measuring future problems can be done with the same exactness. Why shouldn't it be? After all, we have complex mathematical formulas for calculating Value-at-Risk (VaR). It's math; it's proven. "Trust me," say the cybersecurity practitioners.
Single data points, when performing VaR calculations, imply an ability to effectively predict the future with an astounding level of precision. I'm constantly amazed when I see cybersecurity practitioners espousing risk results such as "our risk is $45,890,034 with 99% confidence". In case you missed it, that's a highly precise VaR statement. Cybersecurity practitioners eagerly ask decision makers to make serious spending decisions with these predictive results. What's the use of being precise if we're wrong?
There's a better approach to this problem: accuracy with a useful amount of precision. Accuracy means we are expressing truthfulness, not exactness. For instance, I can guess your weight with some accuracy while expressing little precision by using ranges. I’m more likely to be right about your weight using this technique.
When leveraging accuracy to report risk, we use a range of potential outcomes instead of a single data point. What that means is we can solve both problems at once. We can report a range of risk that no longer seeks to predict the future, while only including enough precision to imply appropriate uncertainty in our inputs. Make no mistake; no matter the model and calculations you use, there is always some degree of uncertainty in the real world. Let's embrace that uncertainty and report it accordingly.
How can we report better results?
What does this look like using RiskLens? Instead of attempting to express 99% confidence in a single value - an incredibly high confidence value in statistical terms - we can use a range of outcomes that are more useful to decision makers. 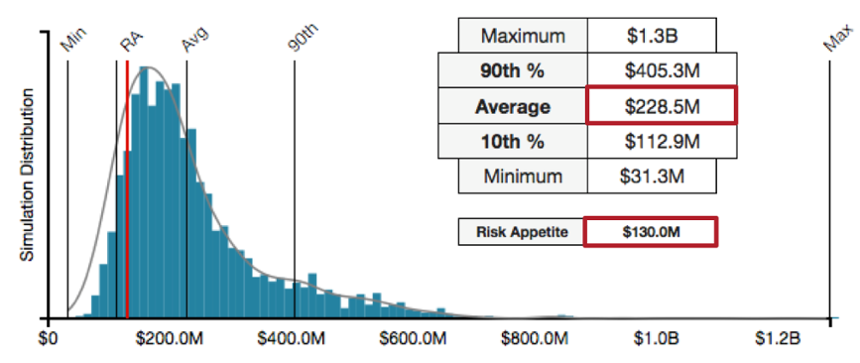
In figure 1, results show a range of possible outcomes for a large data breach considered within an annual time frame. The outcome above, when compared to discrete value reporting, is exponentially more valuable when faced with a risk treatment decision.
This makes sense when you think about your organization suffering a data breach: not all breaches are the same. The range of impact for your organization will vary based on what specific data types and how much of them are stolen. When we focus on a single data point, we are generally forced to talk only about the worst case outcome; which in Figure 1 above would be approximately $1.3 billion. However, reporting only that one data point belies all of the other outcomes that range as low as $31.3 million. A range of outcomes allows us to make varying treatment and remediation decisions across the range, not just the worst-case situation.
To summarize, when analysts use a single date point - like that provided by unfettered VaR calculations - they are forced to report a predictive outcome that shoehorns decision makers into thinking only of the worst case. As you saw in Figure 1, the range of outcomes are reportable using RiskLens which is powered by the FAIR model - one that embraces ranges within VaR calculations.